 Deep learning uses neural networks to build sophisticated models. The basic building blocks of these neural networks are called “neurons”. When a neuron is trained to act like a simple classifier, we call it “perceptron”. A neural network consists of a lot of perceptrons interconnected with each other. Let’s say we have a bunch of inputs and the corresponding desired outputs. The goal of deep learning is to train this neural network so that the system outputs the right value for the given set of inputs. This process basically involves tuning each neuron in the network until it behaves a certain way. So what exactly is this perceptron? How do we train it in Python?
Deep learning uses neural networks to build sophisticated models. The basic building blocks of these neural networks are called “neurons”. When a neuron is trained to act like a simple classifier, we call it “perceptron”. A neural network consists of a lot of perceptrons interconnected with each other. Let’s say we have a bunch of inputs and the corresponding desired outputs. The goal of deep learning is to train this neural network so that the system outputs the right value for the given set of inputs. This process basically involves tuning each neuron in the network until it behaves a certain way. So what exactly is this perceptron? How do we train it in Python?
What is a perceptron?
If you want to understand the concept in a more detailed way, you can check out this blog post that I had published a while ago. Let’s go through a quick refresher here. A perceptron basically takes a bunch of inputs and produces a binary output. These inputs can be weighted depending on the problem at hand. If the output exceeds a certain threshold value, it becomes 1. If not, the output becomes 0. That’s a perceptron for you! Pretty easy, right? Let’s look at the figure below:

Here, the output is computed using the following formula:
weighted sum = w1*x1 + w2*x2 + w3*x3 + w4*x4
The weighted sum is a real number. Now once we set the threshold, the rule would be:
output = 1 if weighted sum > threshold output = 0 if weighted sum <= threshold
This is what we get from a perceptron!
How do we use it?
The interesting thing about perceptron is that we can train it to behave in a specific way. Let’s say we have defined a problem. This means that the inputs and outputs are fixed. We have some inputs which we cannot control, and we desire certain outputs which are dictated by the problem definition. So given this situation, the only things we can control are the weights and the threshold. We can keep changing the weights and the threshold until we get what we want. In machine learning lingo, this process is called “training”.
Let’s consider a simple example. Suppose that you are considering buying a new car right now. For the sake of argument, let’s say that it depends on only 4 factors – price of the car, ease of public transport, your driving skills, and the model of the car. This decision making process can be modeled as a perceptron. Those 4 factors can be the inputs and the output is a yes/no decision. In this input list, you can see that some factors are more important than the others. For example, the price is a crucial factor, so you want to give that the highest priority. This means that the corresponding weight for this input should be higher as compared to others. You might not be so concerned about your driving skills because you are fairly confident about driving a car well. The corresponding weight for this input should be relatively lower. You can keep modifying the weights until you hit the sweet spot.
You can do something similar for the threshold as well. If you increase it, it means that you want all the factors to work for you. If the threshold is high, then the weighted sum might not hit that value unless everything is optimal. This means you are biasing your decision towards not buying the car. If you decrease it, it means that you are training your perceptron to favor the car-buying decision.
How to do it in Python?
We’ll be using a library called neurolab. It is a powerful, yet simple, neural network library in Python. You need to have pip to install this package. If you don’t have pip, you need to install it first. If you are on Mac OS X, it is recommended that you install python using Homebrew. It will automatically install pip for you. You can follow the simple steps given here to install brewed python.
We are now ready to install neurolab:
$ pip install neurolab
Let’s play around with some sample data:
import neurolab as nl
import pylab as pl
input_data = [[0.3, 0.2], [0, 1.3], [1.4, 0.6], [0.5, 1.9]]
output = [[0], [1], [1], [1]]
pl.figure(0)
pl.scatter([x[0] for x in input_data], [x[1] for x in input_data])
pl.xlabel('X-axis')
pl.ylabel('Y-axis')
pl.show()
Put the above piece of code in a “.py” file and run it. When you do, you’ll see the following plot:
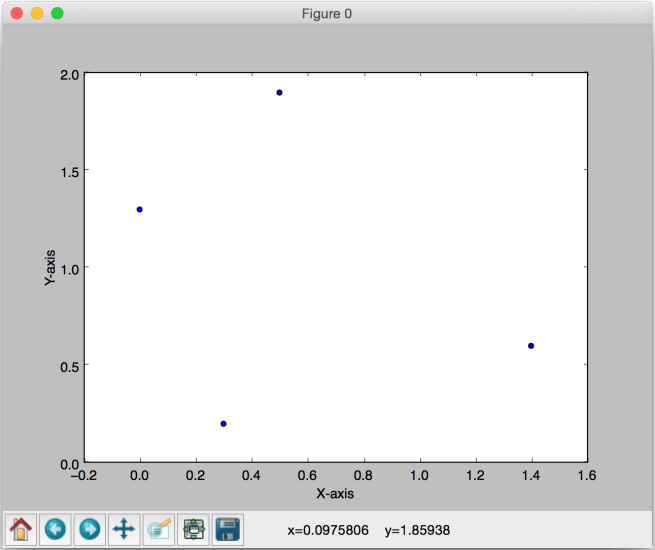
To make it clearer, the figure below indicates the labels and the boundary we would like to see:
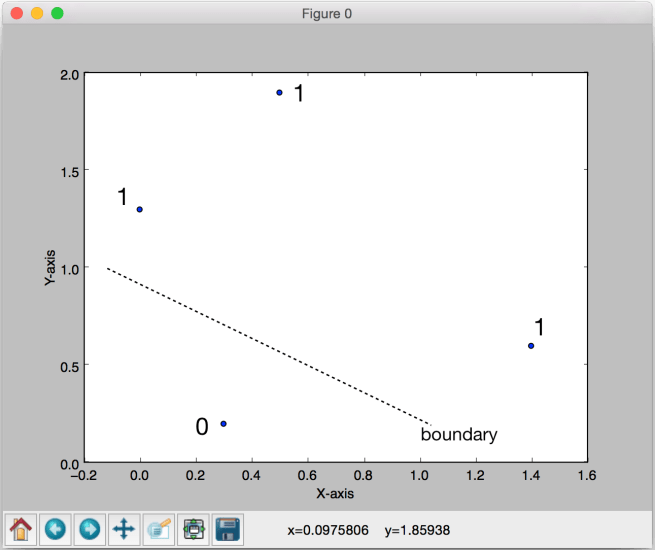
As we can see here, we want to separate the points into two groups.
Let’s create a single-neuron network with two inputs (because we are dealing with 2-dimensional data):
perceptron = nl.net.newp([[0, 2],[0, 2]], 1)
It’s important to understand the above line. In the first argument, the length of the list “[[0, 2],[0, 2]]” is 2, which indicates that there are two inputs. Each item in this list has two elements. The first element indicates the minimum value that our input can take and the second element indicates the maximum value our input can take. Now let’s consider the second argument in the function. The value “1” indicates that there is a single neuron in this network.
Let’s train this perceptron:
error = perceptron.train(input_data, output, epochs=50, show=15, lr=0.01)
The number of epochs indicates the number of training cycles. The argument “show” refers to the printing frequency on the terminal, and “lr” refers to the learning rate of the algorithm. Learning rate refers to the step size that’s taken to adjust the parameters so that we move towards the end goal. Let’s plot the results:
pl.figure(1)
pl.plot(error)
pl.xlabel('Number of epochs')
pl.ylabel('Training error')
pl.grid()
pl.show()
You should see the following plot:

As we can see here, the error went down to 0 in just 4 epochs. Congratulations! You just trained a perceptron in Python. You can change the input data and the output tags to see how it affects the training process.
————————————————————————————————————————–
Is is possible to see the weights assigned to each input in the example shown above?
A silly question [0.3, 0.2], [0, 1.3], [1.4, 0.6], [0.5, 1.9] , are these the four variables and the weight associated to each value? why are we considering those values?
They are the four 2D points chosen at random for the sake of analysis 🙂